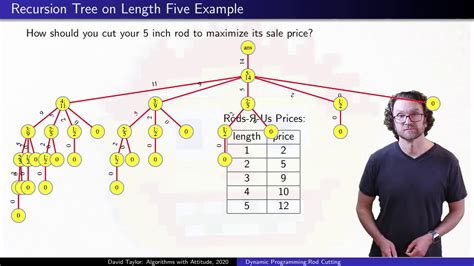
The Cut Rod problem is a classic problem in dynamic programming, a method for solving complex problems by breaking them down into simpler subproblems. It is often used to introduce the concept of dynamic programming due to its simplicity and elegance. The problem statement is straightforward: given a rod of a certain length and a list of prices for rods of different lengths, determine the optimal way to cut the rod into smaller pieces to maximize the revenue.
In more technical terms, if we have a rod of length n and a price list p where p_i is the price of a rod of length i, we want to find the optimal cuts that maximize the total revenue. The problem assumes that the rod can be cut into any number of pieces, and each piece can be sold for the price corresponding to its length. For example, if we have a rod of length 4 and the price list is [0, 1, 5, 8, 9] (meaning a rod of length 1 can be sold for $1, a rod of length 2 can be sold for $5, etc.), we need to determine how to cut the rod to get the maximum revenue.
Natural Solution Approach with Dynamic Programming

Dynamic programming solves the Cut Rod problem by breaking it down into smaller subproblems, solving each subproblem only once, and storing the results to subproblems to avoid redundant computation. The approach involves creating a table where each entry s_i represents the maximum revenue that can be obtained from a rod of length i. For each possible length i from 1 to n, we consider all possible cuts and choose the one that maximizes the revenue.
Bottom-Up Dynamic Programming Solution
A bottom-up dynamic programming solution starts with the smallest subproblems (rods of length 1) and builds up to solve the original problem. The recurrence relation for this problem can be defined as follows: for a rod of length i, the maximum revenue s_i is the maximum of the price of the rod of length i itself and the sum of the maximum revenues of the two pieces resulting from any possible cut. Mathematically, this can be represented as s_i = max(p_i, sj + s{i-j}) for all j from 1 to i-1, where sj and s{i-j} are the maximum revenues for rods of lengths j and i-j, respectively.
| Length | Maximum Revenue |
|---|---|
| 1 | p_1 |
| 2 | max(p_2, p_1 + p_1) |
| 3 | max(p_3, p_1 + p_2, p_2 + p_1) |
| ... | ... |
| n | max(p_n, s_j + s_{n-j} for all j) |

Practical Implementation Considerations

When implementing the solution to the Cut Rod problem, it’s crucial to consider the practical aspects of the algorithm, such as the time and space complexity. The dynamic programming approach has a time complexity of O(n^2) because for each length i, we potentially consider all previous lengths j. The space complexity is O(n) because we only need to store the maximum revenues for rods of lengths up to n.
Code Implementation Example
An example implementation in a programming language like Python could look as follows:
def cut_rod(prices, n):
# Initialize the maximum revenue table
max_revenue = [0] * (n + 1)
# Fill the table in a bottom-up manner
for i in range(1, n + 1):
max_val = float('-inf')
for j in range(i):
max_val = max(max_val, prices[j] + max_revenue[i - j - 1])
max_revenue[i] = max(max_val, prices[i])
return max_revenue[n]
# Example usage
prices = [0, 1, 5, 8, 9, 10, 17, 17, 20]
n = 8
print("Maximum Obtainable Value is", cut_rod(prices, n))
Key Points
- The Cut Rod problem is a classic dynamic programming problem that involves finding the optimal way to cut a rod of a certain length into smaller pieces to maximize the revenue.
- The problem can be solved using a bottom-up dynamic programming approach with a time complexity of O(n^2) and a space complexity of O(n).
- The solution involves creating a table where each entry represents the maximum revenue that can be obtained from a rod of a certain length.
- For each possible length, the solution considers all possible cuts and chooses the one that maximizes the revenue.
- The practical implementation of the solution should consider the time and space complexity of the algorithm.
What is the Cut Rod problem?
+The Cut Rod problem is a classic problem in dynamic programming that involves finding the optimal way to cut a rod of a certain length into smaller pieces to maximize the revenue.
How is the Cut Rod problem solved?
+The Cut Rod problem is solved using a bottom-up dynamic programming approach that involves creating a table where each entry represents the maximum revenue that can be obtained from a rod of a certain length.
What is the time complexity of the Cut Rod problem solution?
+The time complexity of the Cut Rod problem solution is O(n^2), where n is the length of the rod.
As we conclude our exploration of the Cut Rod problem and its solution using dynamic programming, it’s clear that this problem serves as an excellent example of how complex problems can be broken down into manageable subproblems and solved efficiently. The principles and techniques learned from solving the Cut Rod problem can be applied to a wide range of problems in computer science and other fields, making it a fundamental and valuable learning experience for anyone interested in algorithms and problem-solving.